Trabalho de Álgebra II - Modelagem Matemática

Modelagem Matemática

A modelagem matemática surge durante o Renascimento, quando se constroem as primeiras idéias da Física apresentadas segundo linguagem e tratamento matemáticos.

Hoje a modelagem matemática constitui um ramo próprio da Matemática. Na educação matemática, a modelagem matemática firma-se no início dos anos 80, a partir de experiências feitas por um grupo de professores do IMECC/UNICAMP que procuraram considerar a influência dos estudos sócios culturais ao ensinar matemática.

Para Bassanezi (1987), essa idéia foi abordada para esboçar a matemática a partir de temas de contextos sócio-culturais das pessoas.

Muitos cursos de matemática estão inteiramente voltados para a modernização da forma de apresentação da matemática, não se trata como se tem afirmado com frequência de matemática moderna, mas uma forma moderna da matemática de sempre.

Com a chegada do novo milênio a sociedade se vê frente a frente com novos desafios e conseqüentemente a educação, que é reflexo da sociedade, também vem enfrentando desafios, pois na educação é desejada a responsabilidade de propor um novo cidadão que atenta às necessidades e às prioridades desta nova sociedade que está sendo construída.

Neste contexto, a modelagem matemática surge na educação como ferramenta que dá suporte para os desafios do novo milênio. A modelagem matemática não é uma idéia nova, pois sempre esteve presente na criação das teorias físicas e na criação das teorias matemáticas. Seu processo envolve a obtenção de um modelo que pode ser formulado em termos familiares utilizando expressões numéricas ou fórmulas, diagramas gráficos ou representações geométricas etc.

Seja qual for o caso, a solução de um problema, em geral, requer uma formulação matemática detalhada, um conjunto de símbolos e relações matemáticas que procurem deduzir de alguma forma o fenômeno em questão ou problema da situação real, denominados de Modelos Matemáticos.

Para Biembengut (1999) o grande desenvolvimento da ciência nas últimas décadas, deve em parte à aplicação da matemática, isso chamou a atenção para os efeitos que a matemática aplicada e os modelos passaram a ter no ensino. O uso da Modelagem na educação é recente, contudo na última década vem ganhando espaço. Em diversos países, sendo que em alguns deles estão sendo desenvolvidas experiências sobre o ensino das aplicações matemáticas com processo de construção de modelos na formação do professor.

No Brasil ainda são poucas as Universidades que se preocupam em proporcionar aos seus acadêmicos de seus cursos de Licenciatura estágios nas indústrias ou na agricultura, de modo a permitir uma visão mais profunda a respeito das aplicações matemáticas nessas atividades, limitando-se somente a exigir certa quantidade de horas em sala de aula, para servir como estágio, não proporcionando aos acadêmicos experiências com aplicações da matemática, o que possibilitaria uma maior incursão desse profissional no mercado de trabalho. Isso pode se tornar um obstáculo à adoção do estudo com Modelos Matemáticos, levando o acadêmico a não associação de alguns conteúdos escolares que são possíveis de serem relacionados com a sua realidade, tornando dessa forma o ensino da matemática, muitas vezes desmotivado e sem sentido.

A Modelagem Matemática então conforme diz Biembengut (2002), é o meio de fazer interagir os dois conjuntos despertos a matemática, desta forma pode se dizer que Modelagem Matemática é todo processo de abordagem de um problema não-matemático, envolvendo a construção de um modelo ao processo de construção do conhecimento, chamado de Modelagem Matemática.

Segundo Biembengut (1999) o objetivo principal da Modelagem Matemática é convidar o aluno a explorar matematicamente, situações não matemáticas tendo por fim sua formação matemática. Se este processo resulta num modelo matemático, as atividades são também reconhecidas como modelagem.

Para Bassanezi (1998) a modelagem em sala de aula consiste em dividir os alunos em grupos, os quais devem eleger temas de interesse para serem investigados por meio da matemática, contudo acompanhada pelo professor. No entanto não devemos levar o aluno a pensar que só é importante na matemática aquilo que se aplica na realidade cotidiana, pois Bassanezi (2002) ainda afirma que grande parte das idéias matemáticas tem origem em situações empíricas que quando trabalhadas enveredam pelo caminho da estética e quanto mais se afastam da situação de origem, maior o perigo que venha a se tornar em amontoados de detalhes complexos e pouco significativos.

Trabalhar com a matemática no ensino não é somente uma questão de ampliar o conhecimento em matemática, mas sobre tudo de se estruturar a maneira de pensar e de agir do indivíduo.

Da modelagem matemática publicado 6/08/2010 por ANA LUCIA FERREIRA CHAVES em http://www.webartigos.com

Fonte: http://www.webartigos.com/articles/44264/1/Da-modelagem-matematica/pagina1.html#ixzz1IIW4i2vO

Mínimo Múltiplo Comum (m.m.c.)

Dois ou mais números sempre têm múltiplos comuns a eles. 

Vamos achar os múltiplos comuns de 4 e 6: 

Múltiplos de 6: 0, 6, 12, 18, 24, 30,... 

Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,... 

Múltiplos comuns de 4 e 6: 0, 12, 24,... 

Dentre estes múltiplos, diferentes de zero, 12 é o menor deles. 

Chamamos o 12 de mínimo múltiplo comum de 4 e 6. 

Indica-se: m.m.c (4 e 6) = 12

Agora vamos achar os múltiplos comuns de 40 e 60. 

Múltiplos de 40: 0, 40, 80, 120, 160, 200, 240, 280, 320, 360, 400... 

Múltiplo de 60: 0, 60, 120, 180, 240, 300, 360, 420, 480... 

Os múltiplos comuns de 40 e 60 são: 0, 120, 360... 

O número 120 é o menor ou mínimo múltiplo comum dos números naturais 40 e 60. 

Indica-se: m.m.c (40 e 60) = 120. 
Existem outras duas maneiras de calcular o m.m.c de dois ou mais números naturais: 

Vamos começar determinando o menor número natural, diferente de zero, que é múltiplo comum dos números 20 e 40. 

1º) Primeiramente, vamos decompor cada um dos números em fatores primos: 

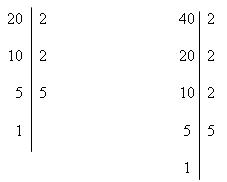Agora, consideramos todos os fatores na forma fatorada, cada um deles com seu maior expoente. 

Neste caso esses fatores são 2³ x 5
 
O produto dos fatores encontrados será o m.m.c procurado, ou seja: 

m.m.c (20, 40) = 2³ x 5 = 40 

2º) A outra maneira de calcular o m.m.c é fazendo uma decomposição simultânea, em fatores primos, considerando os mesmos números 20 e 40. 

Neste processo decompomos todos os números ao mesmo tempo, num dispositivo como mostra o exemplo abaixo. O produto dos fatores primos que obtemos nessa decomposição é o m.m.c. desses números. 

conteúdo extraído

Máximo Divisor Comum (m.d.c)

O maior divisor comum de dois ou mais números é chamado de máximo divisor comum desses números. 

Usamos a abreviação m.m.c

Dois números naturais sempre têm divisores comuns. 

Por exemplo: 

Os divisores de 12 são: 1, 2, 3, 4, 6 e 12. 

Os divisores de 18 são: 1, 2, 3, 6, 9 e 18. 

Os divisores comuns de 12 e 18 são: 1,2,3 e 6.
 
Dentre eles, 6 é o maior. 
Então chamamos o 6 de máximo divisor comum de 12 e 18 e indicamos m.d.c.(12,18) = 6. Agora veja as multiplicações com os números 20, 30 e 40. 



Os divisores de 20 são: 1, 2, 4, 5 10, 20. 

Os divisores de 30 são: 1, 2, 3, 5, 6, 10, 15, 30. 

Os divisores de 40 são: 1, 2, 4, 5, 8, 10, 20, 40. 

Os divisores comuns de 20, 30, 40 são: 1, 2, 5, 10. 

Dentre eles 10 é o maior. 

Então chamamos o 10 de máximo divisor comum de 20, 30 e 40. 
Indicamos m.d.c.(20, 30, 40) = 10.

Conteúdo extraído.

Fatorando um número

De um modo geral, chamamos de fatoração de um número natural, maior que 1, a sua decomposição num produto de fatores primos. 
Para obter a forma fatorada de um número natural através da decomposição, em fatores primos, temos que fazer o seguinte: 

Dado o número 32: 

Dividimos o número 32 pelo seu menor divisor primo. 

Logo, dividimos o quociente obtido pelo seu menor divisor primo. 

E assim por diante até chegar ao quociente 1. 

Veja: 
32:2 = 16
16:2 = 8
8:2 = 4
4:2 = 2
2:2 = 1

32 = 2 x 2 x 2 x 2 x 2 = 25→  forma fatorada   Todos os fatores são primos. 
Exemplo:
As medidas de uma piscina em metros são dados por números primos. Nessa piscina cabem 70 metros cúbicos. Quais são essas medidas? 
Resolução: 
Devemos escrever 70 na forma fatorada 

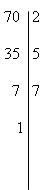
70= 2 x 5 x 7 (forma fatorada) 

Todos os fatores são primos. 

Logo a medida da piscina é 2metros por 5 metros por 7 metros.

Conteúdo extraído.