Mínimo Múltiplo Comum (m.m.c.)

Dois ou mais números sempre têm múltiplos comuns a eles. 

Vamos achar os múltiplos comuns de 4 e 6: 

Múltiplos de 6: 0, 6, 12, 18, 24, 30,... 

Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,... 

Múltiplos comuns de 4 e 6: 0, 12, 24,... 

Dentre estes múltiplos, diferentes de zero, 12 é o menor deles. 

Chamamos o 12 de mínimo múltiplo comum de 4 e 6. 

Indica-se: m.m.c (4 e 6) = 12

Agora vamos achar os múltiplos comuns de 40 e 60. 

Múltiplos de 40: 0, 40, 80, 120, 160, 200, 240, 280, 320, 360, 400... 

Múltiplo de 60: 0, 60, 120, 180, 240, 300, 360, 420, 480... 

Os múltiplos comuns de 40 e 60 são: 0, 120, 360... 

O número 120 é o menor ou mínimo múltiplo comum dos números naturais 40 e 60. 

Indica-se: m.m.c (40 e 60) = 120. 
Existem outras duas maneiras de calcular o m.m.c de dois ou mais números naturais: 

Vamos começar determinando o menor número natural, diferente de zero, que é múltiplo comum dos números 20 e 40. 

1º) Primeiramente, vamos decompor cada um dos números em fatores primos: 

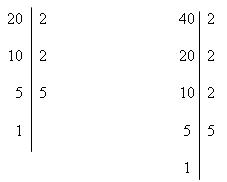Agora, consideramos todos os fatores na forma fatorada, cada um deles com seu maior expoente. 

Neste caso esses fatores são 2³ x 5
 
O produto dos fatores encontrados será o m.m.c procurado, ou seja: 

m.m.c (20, 40) = 2³ x 5 = 40 

2º) A outra maneira de calcular o m.m.c é fazendo uma decomposição simultânea, em fatores primos, considerando os mesmos números 20 e 40. 

Neste processo decompomos todos os números ao mesmo tempo, num dispositivo como mostra o exemplo abaixo. O produto dos fatores primos que obtemos nessa decomposição é o m.m.c. desses números. 

conteúdo extraído